Mass and Density Profiles of White Dwarfs
Published:
This project was to derive and solve the mass-radius relationship for white dwarfs of different chemcial compositions. The interior of the white dwarf was modelled as a near-relativistic degenerate fermi electron gas. This means that the only force stopping the white dwarf from collapsing entirely under its own self-gravity is the repulsion between the free electrons in the gas, as there is no fuel left that the star is able to burn. This force increases as electrons get closet together, but there is an upper limit. As a white dwarf gets heavier, it actually gets smaller, and there is a critical masss above which this electron degeneracy pressure can no longer support the white dwarf. This critical mass is called the Chandrasekhar mass.
The equations of state desribing the mass and density distributions were derived, and then solved using a Runge-Kutta 4(5) process, which is just a fancy way of saying that I made a computer do the hard work of actually solving the equations This produces a relationship between mass and radius, and density and radius for a black hole of a particular mass. This was then repeated for white dwarfs of different total masses, and the mass and outermost radius was recorded for each. The mass at which the radius approaches 0 is the Chandrasekhar mass.
This image shows the track of many of these simulated white dwarfs - the point where an individual line stops is where the total mass and radius is recorded. You can see the lines bunch together at low radius, as the white dwarf gets closer and closer to collapsing.
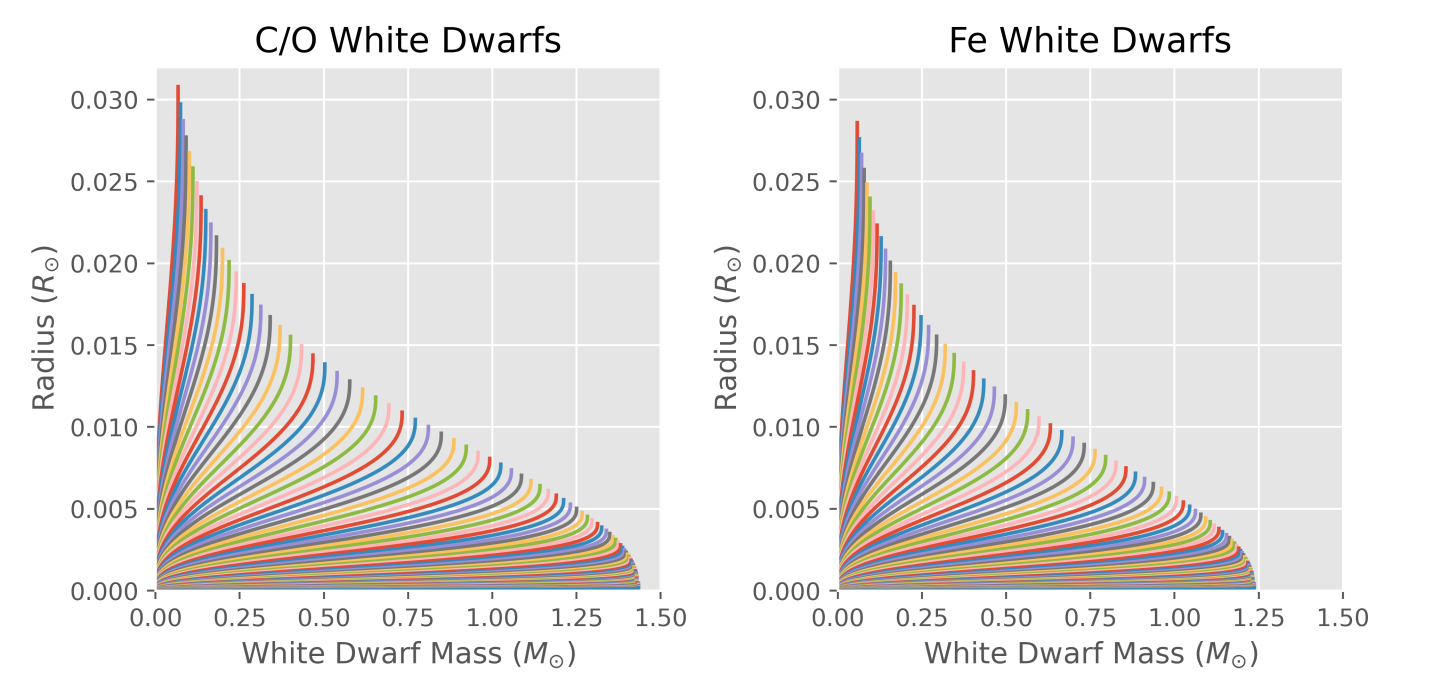
There is a difference depending on what the chemcical composition of the white dwarf is - You can get Helium white dwarfs, or Carbon-Oxygen, or maybe even Iron (Fe) white dwarfs. It depends what the mass and lifecycle of the star that became the white dwarf was. For a common Carbon-Oxygen white dwarf, the maximum mass is about 1.44x the mass of the Sun!
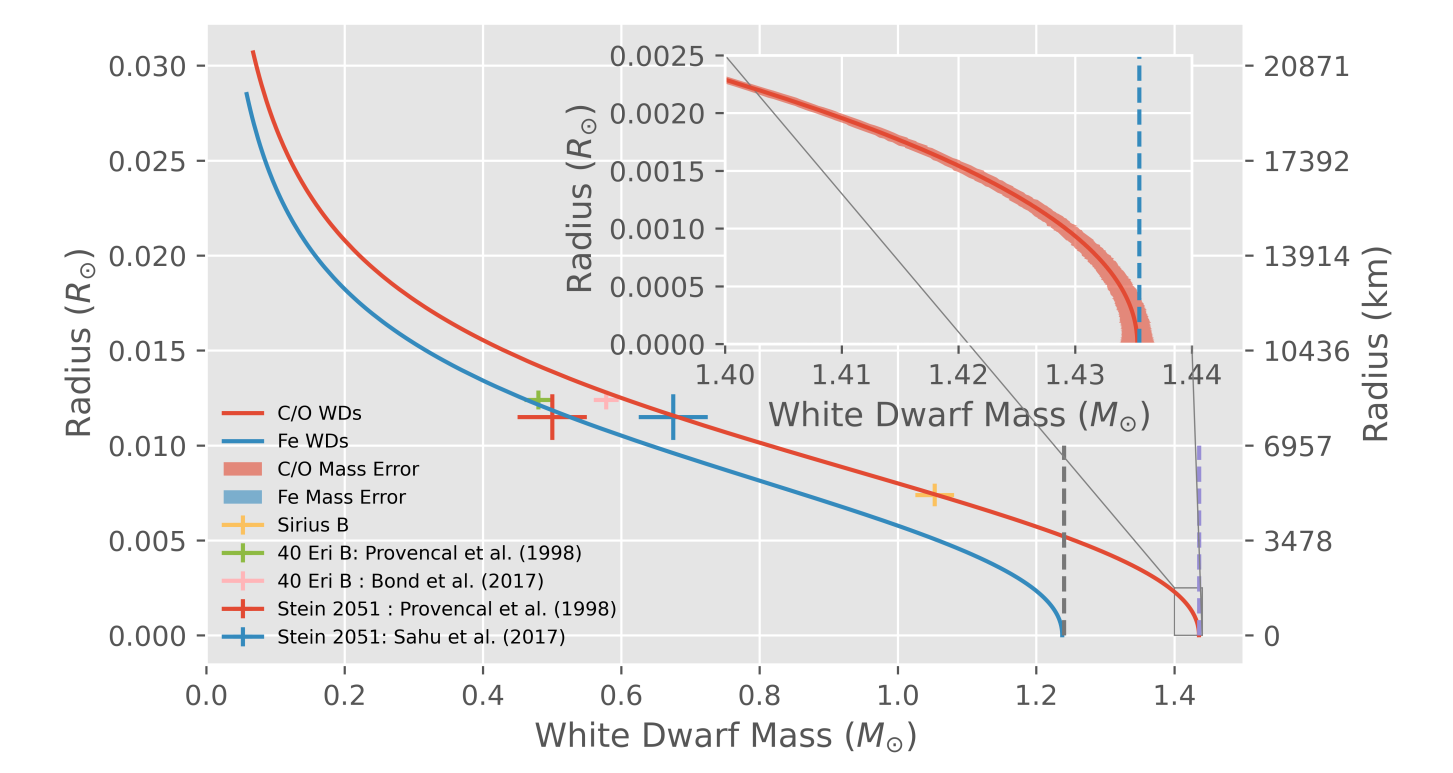
This image shows the track generated from the above image, with some measurements of actual white dwarfs overlaid. If you can accurately measure a white dwarf’s mass and radius you can determine what type of white dwarf it is by where it falls on this track. You can see the white dwarf are normally less than 10,000 km in radius, which is comparable to that of the Earth, but they have a mass closer to that of the Sun!
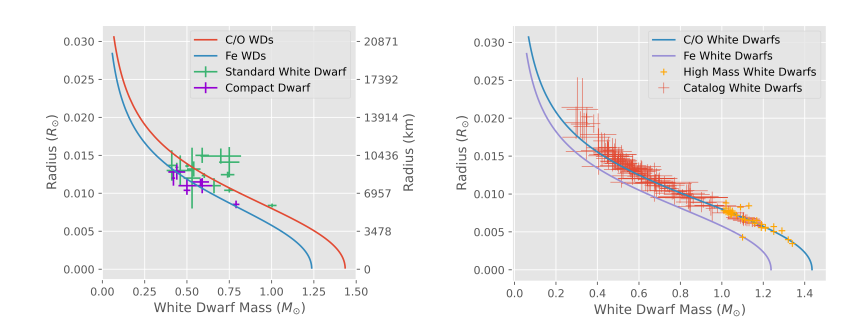
Here you can see a comparison to more white dwarfs, which shows how accurate this relatively simple theory is at describing such complex objects!
If you’d like to learn more, you can find my paper below.
